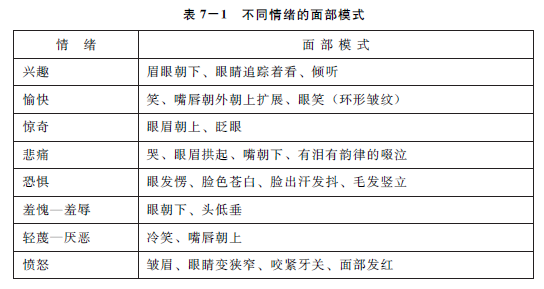
《心理学》第五章 第三节 问题解决

问题解决是最为普遍的一种思维形式。当人们想要实现某个特定的目标，但又不能立即找到实现该目标的合适路径时，其所从事的活动，都可以称作问题解决。需要强调的是，心理学研究“问题解决”时所指的“问题”具有如下性质：人们要完成的任务比较复杂，又没有过完成这类任务的直接经验，人们必须进行认真的思考后，才能找到完成任务的方法和途径。那种比较简单，不需要复杂的思维活动、只需要回忆以往的经验或熟悉的动作就能完成的任务，像“请问您贵姓？”、“您住在什么地方？”等问题，就不包括在问题解决的研究范围之内。

心理学家通常将问题看做一种情境，在这种情境中，个体试图要达到某个目标，就必须发现达到目标的手段。问题的情境也被称为问题空间，一般包含三个重要的组成部分：

（1）初始状态：问题开始时的情境；

（2）目标状态：问题解决时希望达到的状态；

（3）操作：从初始状态向目标状态转化时所需要的一系列操作。

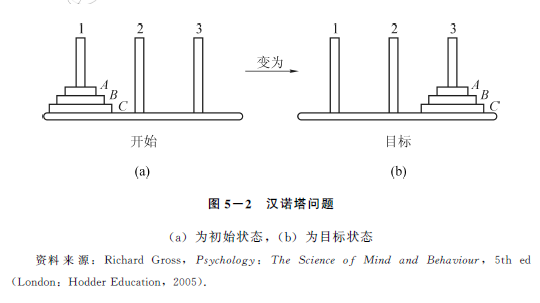
根据这三种成分界定是否清晰，可以将问题分为界定良好问题和界定不良问题。界定良好问题有明确的初始状态和已知条件，有定义清楚的目标，还有明确的途径可以通向目标。比如，著名的汉诺塔问题，就有明确的初始状态和目标状态，解决路径也很明确。（图5-2）一般来说，在学校的考试和测验中，老师让学生解决的问题大都是这种界定良好的问题。

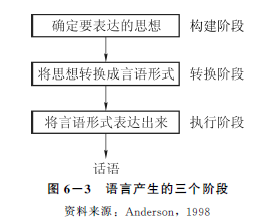
问题解决过程就是克服各种障碍、由初始状态达到目标状态的过程。虽然由于需要解决的问题性质不同，以及个体的个性和经验等方面的差异，人们在解决问题时会表现出不同的特点，但问题解决的思维过程都遵循共同的规律，表现出一定的阶段性。大部分的问题解决都经历提出问题、分析问题、选择策略和检验策略四个相互联系的阶段。

（一）提出问题

提出问题是解决问题的起点。问题广泛地存在于社会生活的方方面面，有的问题比较明显，只需要人们寻找解决问题的方法；还有很多问题是比较隐蔽的，不易被人们发现。能否正确地提出问题会直接影响人们能否正确地解决现实生活中的各种矛盾。有人对问题熟视无睹，有人则善于发现问题。人类历史上的那些杰出的科学家之所以能在各自的领域取得巨大的成就，原因之一就在于他们能在其他人普遍认为没有问题的地方看到问题。“苹果成熟后会掉落到地上”，这是人们熟知的事实，但多少年来没有人对此加以注意。牛顿却从这个普通的现象中产生了这样的疑问：为什么苹果总是垂直落向地面呢？为什么苹果不向外侧或向上运动，而总是向着地球中心运动呢？通过对这些问题的深入思考，牛顿最终发现了万有引力。

（二）分析问题

提出问题后，就要对问题进行分析。如前所述，问题一般都包括初始状态和目标状态。分析问题就是要找到问题的初始状态和目标状态间的差距，从而确定问题解决的方向。分析问题的核心是把握住问题的实质，这将有助于提出更高效的解决方法。比如，有这样一个问题：两个火车站相距100千米，某天下午2时，两个火车头相向开出。一个火车的速度为60千米/小时，另一个火车的速度为40千米/小时，当火车头开始行走时，一只鸟突然出现在第一个火车头前面而向第二个火车头飞去，当鸟到达第二个火车头时，它又立即以原来的速度向第一个火车头飞去。鸟以80千米/小时的速度在两个火车头之间来回飞。问：在两个火车头相遇时鸟飞了多少千米？解题者刚看到这个问题时可能会分析鸟在两个火车头间飞了多少个来回，每个来回飞了多长距离。虽然这样最终也能解决问题，但如果解题者能够作进一步的分析，发现这个问题的实质，就能够更快找到解决问题的方法：直接计算两个火车相遇前行驶了多长时间，将这个时间乘以鸟飞行的速度。

（三）选择策略

通过分析问题，找到问题的实质，还要进一步提出解决问题的具体策略。例如，指挥官为了完成某个作战任务，需要在分析敌我形势的基础上制定具体的作战方案。但是解决问题的方案有时候不是一下就能确定下来的，而是在不断提出策略、验证策略的过程中逐渐形成的。能否提出合理的策略，一方面依赖于个体在该领域的知识经验，知识经验越丰富，就越容易提出合理的策略；另一方面，依赖于个体思维的灵活性，思维越灵活，能够提出的策略就越多。

（四）检验策略

选择的策略是否可行，还必须通过执行策略加以检验。如果执行的结果达到了原来的要求和目标，说明解决方案是正确的，问题得到解决；如果执行的结果没有达到要求和目标，就说明原来的策略是错误的或有缺陷的，问题没有得到解决。这时，就需要解决者提出新的策略，再进行验证，直至达到目标状态。

需要说明的是，以上只是问题解决的一般步骤，在实际的问题解决过程中，人们可能并不会有意识地一步步地思考问题解决的过程，而是将整个的解题过程知觉为一个整体。为了更加清晰地分析出这些解题步骤，心理学家有时会在实验中采用出声思维的方法，让被试用言语报告出问题解决的思路。

问题解决的策略多种多样。一个问题可以用不同的策略来解决，应用哪种策略既依赖于问题的性质和内容，也依赖于人的知识和经验。总的来说，人类主要利用两类基本策略来解决问题：算法策略和启发式策略。

（一）算法策略

算法是指解题的一套规则，它精确地指出解题的步骤。如果一个问题有算法，那么只要按照其规则进行操作，就能获得问题的解。例如，有一把密码锁，密码共有三位，每位有0~9十个数字可选择，你如果想在不知道密码的情况下打开它，就得采用算法策略，逐个尝试三个数字的随机组合。

算法策略的优点是它能够保证问题最终得到解决，但是在解决某些问题时，采用算法策略需要进行大量的尝试，因此效率低下。以下棋为例，如果下棋者应用算法，那么他在下每一步棋前都要考虑所有可能的棋步，并通过计算选择能够最大概率保证获胜的一步棋。虽然从理论上讲，这种下棋方法是可以保证获胜的，但对于人类来说，这种方法是无法应用的。据估算，如果用这种方法来下国际象棋，将涉及10 120种可能的棋步，这已经远远超过了人类的计算极限。因此，当问题较为复杂、问题空间很大时，人们是很难依靠算法这种策略来解决问题的。另外，还有一些界定不良的问题并没有明确的算法，也很难通过算法策略解决。

（二）启发式策略

启发式策略是凭借经验的解题方法，也可称为经验规则。启发式策略与算法策略不同，它虽然不能保证问题一定得到解决，但却常常能高效地解决问题。启发式策略有多种，最常见的是手段—目的分析法。所谓手段—目的分析，就是将需要达到的问题的目标状态分成若干子目标，通过实现一系列子目标最终达到总目标。美国认知心理学家西蒙（Simon）曾系统地研究过手段—目的分析法解决问题的过程，提出它的基本步骤包括：

（1）确定事件当前状态和目标状态间的差距，并找到能够缩小差距的步骤；

（2）如果不能直接达到最终目标，就尝试找到子目标；

（3）寻找达到子目标的方法，实现子目标；

（4）尝试新的子目标。如此循环往复，直至问题解决。

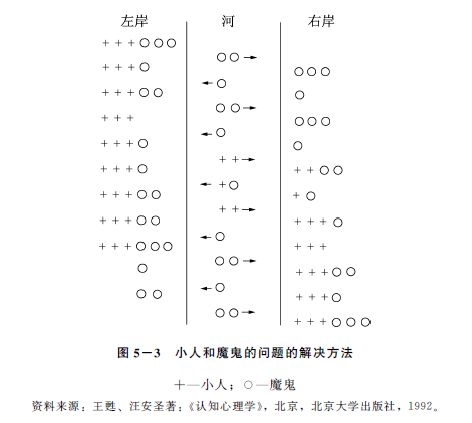
现以著名的“小人和魔鬼的问题”为例来说明这一过程。设有三个小人和三个魔鬼在河的左岸，它们都想过到河的右岸。现有一条小船，一次只能乘坐两个生物。此外，在河的任何一边，一旦魔鬼的数目超过小人的数目，魔鬼将立即将小人吃光。问怎样才能用船将三个小人和三个魔鬼都渡到右岸，而且又不会发生小人被吃掉的情况？

解决这个问题的前六步如下：

（1）从左向右，移动两个魔鬼；

（2）从右向左，移动一个魔鬼；

（3）从左向右，移动两个魔鬼；

（4）从右向左，移动一个魔鬼；

（5）从左向右，移动两个小人；

（6）从右向左，移动一个魔鬼，一个小人。这是关键一步，只有想到这一步，后面的各步才能顺利进行。

（详细步骤见图5-3）

实验研究表明，大部分被试在解决这个问题时，困难往往发生在第六步。原因在于，应用手段—目的分析方法使被试倾向于将更多的人送到对岸，将更少的人送回原岸，从而保证问题解决一直指向目标状态。因而，人们很难想到要使两个人再返回原岸（魔鬼和小人各一个）。实际上，此时所需要的恰是暂时扩大当前状态与目标状态的差异。这个例子说明，手段—目的分析不同于算法，在实际运用时需要一定的灵活性。

影响问题解决的因素有很多，有情境因素也有个人因素，有问题性质也有个体能力方面的原因。以下是心理学研究中关注较多的三类影响问题解决的因素：

（一）问题的表征

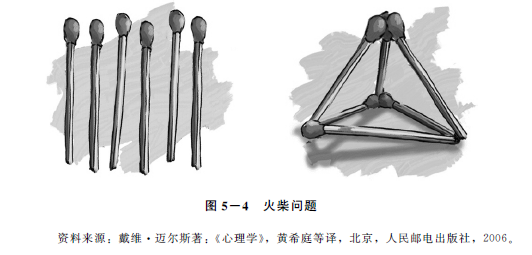
问题表征是问题解决的起始阶段，在该阶段，问题解决者会将任务转化为问题空间，实现对问题的表征和理解。问题的表征依赖于人的知识经验和认知结构，也受到注意、记忆等心理过程的制约。对问题作什么样的表征，这种表征是否适宜，对问题的解决有重要影响。如果问题得不到适宜的表征，那么问题就难于解决或无法解决。比如这样的问题：试用六根火柴摆出彼此相连的四个等边三角形（图5-4）。解决该问题，如果只从平面去表征，问题情境所提供的条件显然不足。因为在平面上构成相连的四个等边三角形至少需要九根火柴。但如果摆脱平面而向立体去表征，问题就可以得到解决了。

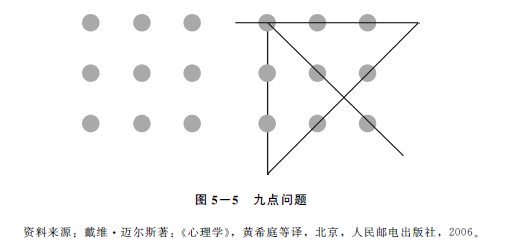
再比如九点问题（图5-5）。有九个排成方阵形的点，试用铅笔画成相连的四段直线，贯穿方阵中的九个点。要解决此问题，如果只从九点方阵的范围内去想，问题是无法解决的。只有改变九点封闭的表征方法，允许直线延伸至九点之外，问题才会得到解决。

（二）定势

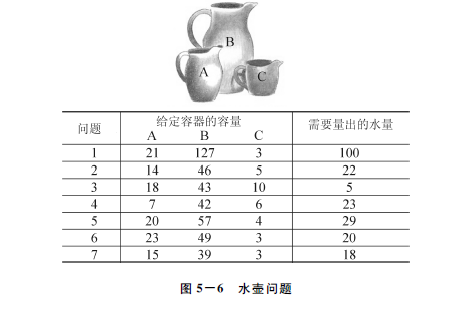
我们在知觉部分曾经讨论过知觉定势的概念，人类的思维过程也存在定势。思维定势是指重复先前的心理操作所引起的对活动的准备状态。在问题解决过程中，如果先前曾采取某种方法解决某类问题并多次获得成功，以后再次遇到同类问题时还会重复采用同样的方法，这就是问题解决过程中的定势。虽然定势有时可以促进问题的解决，但从总体上来说是消极的，它会使问题解决的思维活动变得呆板。美国心理学家卢钦斯（Luchins）曾通过实验证明了定势对解决问题的消极影响。实验要求被试用大小不同的容器（A、B、C）量出规定量的水。各题的条件如图5-6中的表所示。实验分为两组，实验组按顺序做1~7题，控制组只做6、7题。结果发现，实验组中大部分被试在做6、7题时都是采用B－A－2C的方法完成量水任务，只有少数人采用了A－C和A＋C这两种相对简单的方法。而控制组被试在完成6、7题时，都采用了A－C和A＋C这两种方法解决问题。这是由于实验组被试在解决1-5题时，形成了利用B－A－2C这个方法的定势，使得他们在解决6、7题时也采用了相同的方法。

（三）功能固着

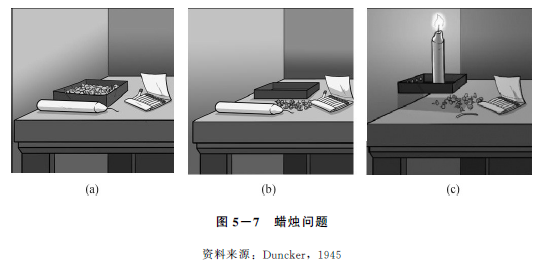
所谓功能固着，是指在问题解决过程中，只看到事物的某种典型功能，而看不到该事物其他方面作用的现象，例如，钥匙是开锁用的，手机是打电话用的。在某些问题的解决过程中，解决者如果能够突破常规，发现事物的某些新功能以适应问题情景的需要，就有可能成功解决问题。比如，钥匙除了可以开锁外，还可以用来拧螺丝；手机除了可以打电话外，还可以用作手电筒。德国心理学家邓克（Duncker，1945）通过实验证明了功能固着对问题解决的影响。实验任务是让被试将燃烧的蜡烛固定在墙上，保证蜡烛不会掉下来。他提供给被试的材料包括蜡烛、火柴、纸盒、图钉等。实验组被试拿到的材料中，纸盒是作为容器使用的，里面装有图钉等物品，如图5-7（a）所示；控制组被试的材料都散放在桌子上，纸盒是空着的，如图5-7（b）所示。正确的解决方法如图5-7（c）所示。邓克发现，纸盒里装入东西后再给被试，会大大增加问题的难度，实验组被试在解决问题时所花费的时间要比控制组被试长很多。因为此时被试会将纸盒的功能固着为一个容器，而不是可以参与问题解决的物体。有意思的是，当让五岁的孩子解决蜡烛问题时，他们几乎没有表现出任何的功能固着。很明显，这是因为他们对很多东西的固定用途还没有形成足够的经验。